|
citace 4.5.2024 - 16:04 - Jan Dusatko:
Zjednodušeně ...
1/ cely okruh moze byt laminarne prudenie, turbina/piest moze byt podla potreby
2/ kvapalinu uvazujem prakticky idealnu. predbezne hovorme o vode. (aj bez toho je to komplikovane) napriklad teploty okolo 90/95°C
A tepelna izolacia ja fajn, lebo teplota okolia je 92,5°C, takze prakticky bez tepelnych strat.
ohrievam stale rovnake mnozstvo hmoty za sekundu o rovnaky rozdiel teplot.
suhlasim, ze dva krat viac hmoty/sekundu, dva krat viac enrgie za sekundu.
ALE ja ohrievam stale rovnake mnozstvo za sekundu. nemenim prietok Qv, len vysku okruhu.
3/ vyhol si sa otazke.
Ak mam okruh s prietokom Qv, jeden stlpec 90°C a druhy stlpec 95°C, tak na ohrev potrebujem vykon P0. Z tohto okruhu s vyskou h1 odoberam turbinkou malicky miniaturny vykon P1.
Ak mam druhy okruh tiez s rovnakym prietokom Qv a teplotami 90/95, len s vyskou 2x h1, tak na jeho ohrev potrebujem stale len vykon P0. Akurat mozem odoberat vykon 2x P1, lebo mam vysku 2x h1 ?
A nech to nemotame s poctom turbin tak v druhom pripade pouzijem 2x vacsiu turbinku
4/ otazka 3) smeruje ci pre 3x h1 mam 3x P1
a ci pre n xh1 mam nx P1
|
|
ALE ja ohrievam stale rovnake mnozstvo za sekundu. nemenim prietok Qv, len vysku okruhu.
- Jedná se o rovnováhu mezi přijatou energií, časem a objemem tekutiny
3/ vyhol si sa otazke
- Ne, nevěděl jsem tvoje požadavky. Takže, pokud máš dvakrát větší sloupec, je rozdíl energií daný rozdílem hustoty tekutin, výškou vodního sloupce a gravitačním zrychlením. Na to ti stačí spočítat objem válce a rozdíl daný tepelnou roztažností (pro zjednodušení si představ, že se ti ten válec protáhne o daný rozdíl). Odebereš tu část, která přesáhne délku a spočítáš rozdíl hmotností. Tím máš daný rozdíl hustot a díky gravitačnímu zrychlení i rozdíl energií. Část odeberou ztráty v potrubí.
- Tedy můžeš odebírat výkon blížící se dvojnásobku výkonu první turbíny.
4/ s jistou mírou přesnosti lze tvrdit, že pro 3x vyšší výšku budeš moci odebírat téměř 3x, pro 4x vyšší výšku téměř 4x ...
Problém ti bude dělat jenom strýček Pascal, protože to co tu je nelineární je hydrodynamický odpor, zapříčiněný tlakem v potrubí (výška * hmotnost) a na uvedeném závislý. Jinak máš víceméně pravdu.
|
|
citace 4.5.2024 - 20:25 - Jan Dusatko:
...4/ s jistou mírou přesnosti lze tvrdit, že pro 3x vyšší výšku budeš moci odebírat téměř 3x, pro 4x vyšší výšku téměř 4x ...
Problem bol ak som pre "n x" definoval n ako podiel vykonu na ohrev a energie ziskanej z turbinky. (lebo sa to blizi perpetuum mobile)
netrvdim, ze to je perpetuum mobile, len sa snazim pochopit ten cyklus.
Ale spravidla sa neviem dostat v diskusii ani po to, ze pre 4 nasobnu vysku h1 bude ekvivalentny vykon cca 4x P1
Kedze ta povazujem za odbornika, som vdacny za tvoj nazor.
Skusil som fyzikalne forum https://www.physicsforums.com/threads/too-much-energy-thought-experiment.1062398/#post-7084010 kde mi chceli poradit, ze
aby zostal zachovany zakon zachovania energie,
tak ak dodam teplo P0 do okruhu a vychladim teplo Pcooling, pricom som turbinkou odobral akusi energiu P1,
tak musi platit P1 + Pcooling = P0
lenze to by sa mala ochladzovat voda po prechode turbinkou? Take nieco si nepamatam a zatial som odpoved nedostal, kde by sa ta voda mala vychladit, aby mi stacil mensi ochladzovaci vykon.
Ja nechcem spochybnovat zakon zachovania energie, ale ja som sa tesil na nieco v style P1 + Pcooling = P0 +XY
Teraz na mna skusaju, ze dole musi byt ohrievaci vykon P0 vacsi ako chlodiaci vykon Pcooling hore, lebo hydrostaticky tlak. Lenze ak wiki neklame, tak na uchladenie budem potrebovat 4215 J / K /kg, zatial co na ohrev mi postaci 4165 J/kg/K prave pre hydrostaticky tlak 200bar.
(https://en.wikipedia.org/wiki/Heat_capacity, April, 2024)
|
|
Martine, nejsem odborník. Ale mám rád konkrétní ukázky, proto si dovolím lehce výpočtů. Pokud je někdo odborník, měl by mne opravit, aby nevznikl nějaký šum. Prosím, ber to jako přirovnání, které by mohlo pomoci situaci vyřešit.
Dle mého tu vznikl problém s přístupem k energiím. Voda má potenciální a kinetickou energii, stejně jako energii dodanou ohřevem a stejně jako jakákoliv jiná hmota energii hmoty jako takové. Ale v tuto chvíli nemůžeš počítat energii samostatné vody, ale celého systému. A ten musí splnit určité podmínky.
Budeme mít nějaký kotel dole, 10m trubky o poloměru 1cm a nahoře radiátor, který je zaplaven až po přívod ohřáté vody. Ten splní tvoje teplotní požadavky. Pokud dobře počítám
- Válec o je 2PiR*H=3,14*20*10000=3,1415dm^3 nebo jinak litrů
- DV = 0,00019*3,1415*5=0,002l = 2ml, jinak také 0,06% změny objemu
- 2ml váží příbližně 2g (zanedbám vliv teploty, tohle platí pro vodu o teplotě 4˚C)
- 2g vody v tíhovém poli Země vytváří sílů ~0,02N
- v tvém případě je to mizivá síla, kterou sníží hydrodynamický odpor. Proto potřebuješ vychladit studenou vodu na co největší rozdíl. Pro rozdíl 50˚C to bude 29ml a síla 0,29N, pro rozdíl 80°C pak 47ml a 0,47N (přibližné výpočty). Na základe uvedených údajů jsi schopen dopočítat přibližnou rychlost proudění. K tomu je dobrá Bernouliho rovnice, rozdíl výšky sloupců (tedy o co je řidší teplá voda proti studené) je to co potřebuješ k výpočtu. Tedy musím vypočítat výšku válce (potrubí), kterou naplní 2ml vody. Když to zjednoduším, tak vezmu výšku 10 000 * 0,06% = 6mm.
Znovu si to zjednodušuji. Tlakové ztráty zanedbám (přestože výška sloupce 10m znamená 10 atmosfér a to už nějaký odpor vznikne, naštěstí téměř netřeba počítat dynamický tlak), plocha skrze kterou projde nějaký objem je 62mm^2. Z toho mi vychází rychlost cca 0,03 mm/s (doufám, že jsem to počítal správně). To bude poníženo odporovými ztrátami. V tomto případě bude proudění prakticky laminární, ale pochybuji, že se turbína při těchto rychlostech vůbec bude pohybovat. Řešením by bylo zůžení průřezu potrubí v místě turbíny, což zdvihne rychlost proudu, na druhou stranu sníží tlak. Pokud tu nějaký pohyb bude, bude turbína brzdit výměnu vody mezi sloupci. To znamená, že se bude tvářit jako zvýšený odpor potrubí. |
|
Dakujem, ja si myslim, ze mam chybu prave v tej potencialovej energii.
to ostatne maly objem pomaly prietok vies odoberat napr. piestom, ak existuje rozdiel talkov. Samozrejme s ucinnostou piestu
ale je to myslienkovy experiment, takze piest nie je problem
|
|
citace 3.5.2024 - 17:31 - Martin Jediny:
takze ono sa musime najprv dohodnut, ze co to je samotazka.

Mám otázku. Vznikne nejaký rozdiel v dvoch prípadoch, keď tú "turbínku" umiestnime do "červenej" trubky ktorou ohriata kvapalina stúpa, a keď ju umiestnime do "modrej" ktorou studená kvapalina klesá?
..
Tak laicky.
Ak bude turbínka v "modrej". Tak funguje ako "vodná elektráreň", medzi dvomi nádržami umiestnenými v rôznej výške.
A "červená časť" bude jednoduchý tepelný stroj, ktorý pomocou tepla iba dopravuje kvapalinu hore.
Nepočítalo by sa takéto usporiadanie, trochu ľahšie? [upraveno 5.5.2024 10:21] ____________________
slavomir.fridrich@azet.sk |
|
rozdiel je, hoci to je stale voda a vodna turbinka.
Vykon = objemovy prietok x rozdiel tlaku vstup/vystup x ucinnost
a ty mas rozdiel v objemovom prietoku.
pretoze ohriata voda ma mensiu hustotu.
preto ak zachobam ostatne parametre, tak v cervenom okruhu bude vykon o trochu vacsi.
A pri plynovej turbine vyrazne |
|
Domnievam sa, že tento problém.
citace:
lenze to by sa mala ochladzovat voda po prechode turbinkou? Take nieco si nepamatam a zatial som odpoved nedostal, kde by sa ta voda mala vychladit, aby mi stacil mensi ochladzovaci vykon.
"Do teba hodil" niekto kto, tú turbínku dal do "červenej", a navyše si predstavoval že pracovné médium nebude voda, ale plyn o vysokej teplote a tlaku.
 ____________________
slavomir.fridrich@azet.sk |
|
Ale cely problem stoji na otazke...
...kolko tepla protrebujem, ak ohrievam 1kg vody z teploty 90°C na 95°C pri konstantnom tlaku.
Ak mam tlak 1 bar
Ak mam tlak 100 bar
odporucili mi tabulky...
https://webbook.nist.gov/cgi/fluid.cgi?P=10.0&TLow=90&THigh=95&TInc=1&Digits=5&ID=C7732185&Action=Load&Type=IsoBar&TUnit=C&PUnit=MPa&DUnit=g/ml&HUnit=kJ/kg&WUnit=m/s&VisUnit=uPa*s&STUnit=N/m&RefState=DEF
Ak to spravne odcitujem, tak na spad 90/95 pri tlaku
0,1MPa potrebujem na ohrev 1kg vody 21,04 kJ (len poznamka Cp=4,2102, dRo= 0,96531-0,96189=0,00342 g/ml)
a pri tlaku 10MPa potrebujem na 1kg vody 20,93 kJ (len poznamka Cp=4,1884, dRo= 0,96978-0,96641=0,00337 g/ml)
[upraveno 5.5.2024 14:20] |
|
Má tá otázka vôbec zmysel, pri matérii menom voda?
Voda je sakramentsky ťažko stlačiteľná..
Kdesi som videl tvrdenie, že ľahšie je zmeniť objem vody ochladením ako "presovaním".
..
Neviem či nefantazírujem.
Ale pri naozaj veľkej výške okruhu, by tam nedochádzlo k "fázovým zmenám", keď sa voda v dôsledku poklesu tlaku v "stĺpci" vyvarí a premení na paru?
V zadaní musí byť uvedené, či sa jedná o vodu ako vodu, alebo o nejakú "ideálnu nestlačiteľnú kvapalinu".. ktorá ale rozhodne nebude voda. [upraveno 5.5.2024 18:13] ____________________
slavomir.fridrich@azet.sk |
|
citace 5.5.2024 - 01:59 - Jan Dusatko:
Martine, nejsem odborník. Ale mám rád konkrétní ukázky, proto si dovolím lehce výpočtů...
Momentálne sme sa zasekli na privela energii v radiatore. To ze som chcel nejaku energiu este aj odoberat som zatial radsej zatial vypustil.
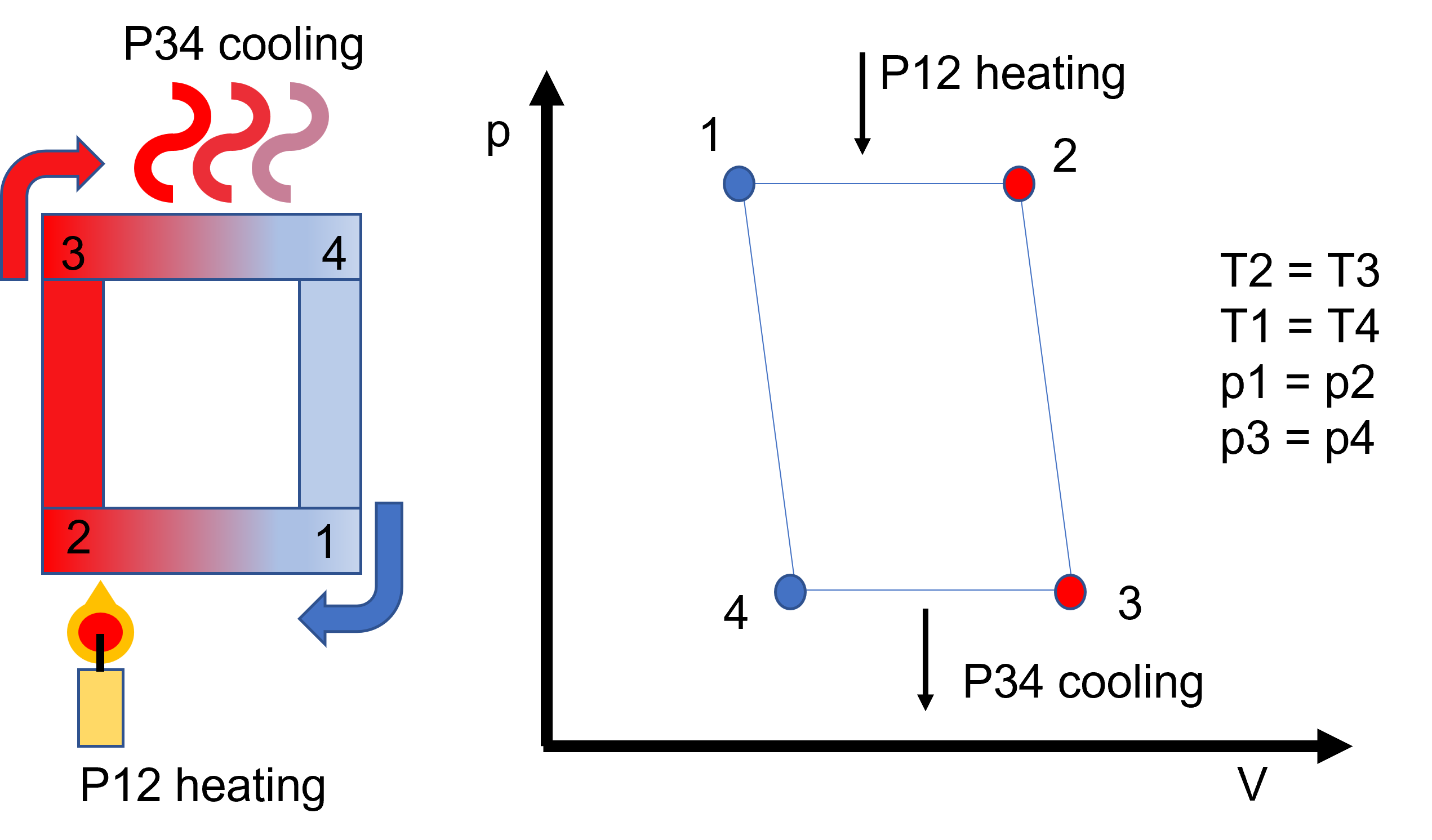
prietok 1kg/s
línia 1-2 dolný prepoj, tlak 10MPa. Ohrev P12= 20,93 kW ? +36W ?
bod 1: 90°C, Ro1=0,96978 g/ml, Enthalpy: 384,73 kJ/kg , Cp=4,1837 J/(g.K)
bod 2: 95°C, Ro2=0,96641 g/ml, Enthalpy: 405,66 kJ/kg , Cp=4,1884 J/(g.K)
línia 2-3 gravitačné stúpanie teplej vody bez čerpadla. Výška 1000m
línia 3-4 horný prepoj, tlak 0,1MPa, Chladenie P34= 21,04 kW
bod 3: 95°C, Ro3=0,96189 g/ml, Enthalpy: 398,1 kJ/kg , Cp=4,2102 J/(g.K)
bod 4: 90°C, Ro4=0,96531 g/ml, Enthalpy: 377,06 kJ/kg , Cp=4,2052 J/(g.K)
línia 4-1 gravitačné klesanie chladnej vody. Výška 1000m
Urobil som chybu.
Voda je totiz na tejto skale stalcitelna potom T2 > T3 [upraveno 5.5.2024 22:45] |
|
citace 5.5.2024 - 18:39 - Martin Jediny:
Urobil som niekde chybu?
Domnievam sa, že "chybu", asi v tom zmysle ako má Alcubierrov pohon.
To je všeobecne populárna a prijímaná teória, akurát si źiada ako súčiastku "matériu s negatívnou hmotnosťou", ktorú neviem skade nabrať.
Tvoj stroj, si asi źiada ako pracovné médium, akúsi teoretickú "kvapalinu" so špecifickými vlastnosťami.. ____________________
slavomir.fridrich@azet.sk |
|
citace 5.5.2024 - 14:25 - Slavomír Fridrich:
Neviem či nefantazírujem.
Ale pri naozaj veľkej výške okruhu, by tam nedochádzlo k "fázovým zmenám", keď sa voda v dôsledku poklesu tlaku v "stĺpci" vyvarí a premení na paru?
Mno.. negatívny Joule-Thomsonov koeficient voda má, ale vraj len pri "nízkych teplotách".
citace:
https://link.springer.com/article/10.1007/s11242-014-0379-3
Pretože kvapalná voda má pri nízkych teplotách záporný Joule-Thomsonov koeficient, pri konštantnom gravitačnom potenciáli sa voda ochladzuje, keď sa stláča a ohrieva, keď sa rozpína. Ak ignorujeme gravitačnú energiu, transport samotnej entalpie vedie k ohrevu vody o 2
C na kilometer, keď sa zdvihne z hĺbky. Opravená energetická bilancia prenáša metalpiu, čo je entalpia plus gravitačná potenciálna energia. Hoci jednoduchšia forma vedie k malým zmenám v teplotnom profile pre typické simulácie, existuje niekoľko prípadov, kedy sa tento efekt môže ukázať ako dôležitý. Najdôležitejší vplyv chybnej formy je pravdepodobne v oblasti výroby geotermálnej energie, kde by vytvorenie niekoľkých stupňov tepla v simulácii mohlo viesť k nesprávnemu výpočtu účinnosti elektrárne.
____________________
slavomir.fridrich@azet.sk |
|
citace 5.5.2024 - 18:39 - Martin Jediny:
Urobil som chybu.
Voda je totiz na tejto skale stalcitelna [upraveno 5.5.2024 22:21]
Nemôžem si pomôcť.
Nesmúť.
Teoreticky. Keby si použil, ako pracovnú látku amorfný ľad. (furt je to voda) Niekde, na planétke Pluto.
Síce by to fungovalo, pomalšie ako Alpské ľadovce.
Ale bol by s toho omnoho zložitejší a viac sci fi problém.
Ktorý by možno zaujal ľudí, dokonca viac ako Alcubierre drive.
 ____________________
slavomir.fridrich@azet.sk |
|
Čisto prakticky.
Tie nadšené komentáre, po prelete New Horizonts, že na Plute bude pod povrchom oceán tekutej vody , sa akosi vytratili.
Veku toho stále sa obnovujúceho "bublajúceho" oceánu dusíkovej zmrzliny, nezodpovedá nijaký pochopiteľný obsah nejakého známeho izotopu, ktorý by sa tam rozoadal a poháňal proces.
Ten tepelný motor, čo tam "dodnes" funguje, je fakt "sci fi".
 ____________________
slavomir.fridrich@azet.sk |
|
@Martin Jediny
"Odpovedal" si, pánovi Dusátkovi..
Mne nie.. ____________________
slavomir.fridrich@azet.sk |
|
naposledy som reagoval 5.5.
1/ odvtedy len prebehnem forum, ci netreba nieco precistit, ale nestiham nic pridavat
2/ neviem na tvoje posledne prispevky prinosne zareagovat |
|
@Martin Jediny
Prepáč. Dalo by sa povedať, že odpánov Bill Nelson a Tory Bruno, som sa dozvedel "príliš veľa informácií" a trochu ma to rozhodilo. ____________________
slavomir.fridrich@azet.sk |
|